Part 3: The Chess Board
Functional Requirements (FRs)
Like in real world chess everything starts with a board also in computer chess the internal representation of the chess board is a central component of a chess engine.
Let's summarize the functional requirements of the chess board component.
It has to store the internal state of the game which means
- the location of the white and black pieces
- the side to move
- the castling rights for both sides
- the en passent square (if any)
The board must be able to make and unmake moves, so it can change its internal state when it gets a move as input.
The board must be able to generate a list of all legal moves for the side to move (move generator).
Besides those core requirements it is useful if the board
- has a record of previous boards within the same game (like a history)
- stores the turn number
- stores the moves that were executed from the start position up to the actual position
- recognizes a check, checkmate or stalemate
- has an numeric id used to determine whether two boards are the same w/o comparing every square content
- is able to initialize itself into the start position or any other legal midgame position

Several common internal board representations exist. It is possible to implement it via a simple squares[8][8] array more advanced arrays up to BitBoard representations.
All are valid and there are pro and cons for all. Every chess engine programmer will have to make an fundamental architectural decision which representation he implements.
For instance the squares[8][8] implementation is very natural and easy to implement and to debug as it very much aligns to the human picture of a chess board. Its cons are that you need two parameters to identify a square (file and rank) and when generating moves you have to do a lot of "off the board" detection.
BitBoards align very much to the computers ways of perceiving a board, so they are fast and it is possible to do fancy stuff with them but it is hard to debug them as to see a board as a combination of 12 64 bit integers is not so easy for the average human.
Another common implementation method for those programmes who want to avoid bitboards is called 0x88, which is an advanced square centric implementation. I can't comment further on it as I never used it but here are good tutorials out there.
For the course of this tutorial we will use a combination of squares and bitboards to represent the board. So we have to maintain a bit of redundant information (bitboards and squares basically contain the same information) but depending on the type of information we need we can always choose the fastest way to access it.
The square centric representation of the board
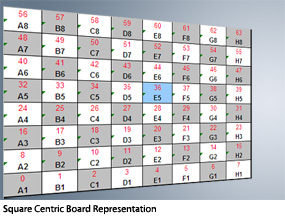
We use a single array of 64 squares to represent the board. Each square contains either a piece or is empty. We start indexing at 0 which represents the square A1, continue with 1 = B1 until 63 = H8.
Each cell in this array holds the information about the piece placed on the corresponding square or that the square is empty.
The bitboard representation of the board
For every piece type (White Pawn, White Knight … Black King) we use a 64 bit integer. Bit 0 (the least significant bit) represents square A1, Bit1 = B1 and Bit 63 = H8. If this bit is set to 1, it means a piece of the specify type is located on that square, 0 means it is not on that square.
Example:
BitBoard W_ROOK = 3 (binary 0000…00 0011) means the square A1 and B1 contain a white rook and no other squares contain a white rook.
BitBoard W_PAWN = 65280 (binary 0000…1111 1111 0000 0000) means all white pawns are on their initial squares (A2 .. H2)
To speed up the calculation later we also maintain some helper bitboards like
- emptySquares (a bitboard where a 1 bit specifies an empty square)
- occupiedSquares (a bitboard where a 1 bit specifies an occupied square)
- whitePieces (a bitboard where a 1 bit specifies a white piece)
- blackPieces
The remaining stuff
The remaining properties of our functional requirements we store simply as class properties of the board.
The source code
While developing the engine you define a lost of types and constants. I strongly recommend creating a special unit or header file for them so you can maintain them centrally and do not run into a cross reference issue where two parts of your program need access to constants defined it the other.
I also recommend using specialised types wherever possible. This makes the code much more readable, facilitates debugging and let the compiler spot a lot of errors already at compile time.
// BitBoard = Int64 (long long) typedef long long TBitBoard; typedef long long int64;// SQUARE Identifiers enum ESquare {A1,B1,C1,D1,E1,F1,G1,H1, A2,B2,C2,D2,E2,F2,G2,H2, A3,B3,C3,D3,E3,F3,G3,H3, A4,B4,C4,D4,E4,F4,G4,H4, A5,B5,C5,D5,E5,F5,G5,H5, A6,B6,C6,D6,E6,F6,G6,H6, A7,B7,C7,D7,E7,F7,G7,H7, A8,B8,C8,D8,E8,F8,G8,H8,ER};
inline ESquare operator++ (ESquare& square) { return (ESquare)(square+1); } inline ESquare operator++ (ESquare& square, int) { ESquare old = square; square = (ESquare) (square + 1); return old; };
// Piece Identifiers enum EPiece {EMPTY,W_PAWN,W_KNIGHT,W_BISHOP,W_ROOK,W_QUEEN,W_KING, B_PAWN,B_KNIGHT,B_BISHOP,B_ROOK,B_QUEEN,B_KING,INVALID};
inline EPiece operator++ (EPiece& piece) { return (EPiece)(piece+1); } inline EPiece operator++ (EPiece& piece, int) { EPiece old = piece; piece = (EPiece) (piece + 1); return old; };
Please note: In c++ when using an enumeration you can't enumerate it by default because an enumertion is just a collection of things where an mathematical addition does not always make sense. In our case it does make sense. I want to be able to loop through all the squares later e.g. for (sq=A1; sq<=H8; sq++) ; . And in order to do that we have to define the ++ operator for our new type.
The Board Data Types itself
// Opponent Colors enum EColor {WHITE,BLACK,NONE};
/******************************************************************* Holds the piece location status of the board in BitBoards per Piece *******************************************************************/ struct TBoardBB { // Holds the piece information per square EPiece squares[H8+2]; // Bit Boards for Pieces TBitBoard pcs[B_KING+2]; // Utility BitBoards TBitBoard emptySquares; TBitBoard occupiedSquares; TBitBoard pcsOfColor[BLACK+1]; };
struct TBoardState { int64 hash; intlastTriggerEvent;// ply whith pawn move or capture int castelingRights; ESquare enPassentSquare; TMove move; bool inCheck; int repetitions; };
/******************************************************************* TBoard : a powerfull class that represents the actual board this class is responsible for legal move generation and move execution *******************************************************************/ class TBoard { public: TBoardBB bb; EColor sideToMove; int currentPly;
TBoard(); ~TBoard(); private: TBoardStateHistory *boardHistory; }
Please note: The TBoardStateHistory is a pointer to a list of TBoardState objects.
In this example the board state (with the casteling rights ...) is stored in the BoardStateHistory list, so the current board state is always the last entry in that list, but we have also all previous board states available. This is important when taking moves back. Consider the case where you move with the white king from square E1, after that move white does not have castling rights anymore. But when you take the move back you must restore the original casteling rights and you don't know them when you did not save them. Now when unmaking a move you simply delete the last entry in the state history list and you have the previous board state with the corrects casteling rights restored.
One last thing
Now where we have the board defined we place the board creation in the constructor of our TChessEngine class with
board = new TBoard();
and destroy it in the TChessEngine destructor.
So what did we do here
We defined essential new data types for our chess engine for squares, pieces and colors. We also created a board class definition, that will contain all the necessary information about the current state of the board. We did not implement any code so far. The constructor and destructor of TBoard are still empty.